알고리즘 코딩기법 - 3. 재귀호출

안녕하세요..

저번 포스팅에서 예고해드린데로 이번에는 재귀호출에 대해서 다뤄볼까합니다.
물론 멤버십에 계신분들중에 재귀호출을 어려워 하실 분들은 없으리라 생각하는데요, 학교에서 주위를 살펴보면 재귀호출을 잘 못하는 친구나, 후배나, 등등 많은 것 같습니다. 그 만큼 재귀호출이 직관적으로 이해가 잘 안되는 부분인가 봅니다. C++과 싸우다 보면 포인터에서 한 번 좌절을 하게 되고 포인터를 넘고나면 재귀호출이 또다시 태클을 건다는.. 뭐 그런 전설이 내려오는데요.. 저도 지금 재귀호출을 어떻게 다뤄야할지 막막합니다 ㅠㅠ

뭐.. 어쨌든..... 각설하고 시작하겠습니다.

 

 

재귀(Recursion)

주어진 문제를 재귀적으로 푼다는 말은 문제의 답이 그 문제와 동일한 형태의 더 작은 부분문제(sub problem)의 답에 의존적(dependency)이다 라는 의미를 가지고 있습니다.

흠.. 무슨말인지 모르겠습니다. 이해를 돕기 위해 쉬운 예를 들어 보겠습니다.

레고블럭으로 만든 커다란 작품이 있습니다.
누가 저 작품에 레고블럭이 몇 개가 쓰였는지 물어봅니다.
도저히 한눈에 레보블럭이 몇 개가 쓰였는지 알지 못하겠습니다.
레고를 쪼갭니다.
아직 각각이 몇개씩인지 모르겠습니다.
다시 레고를 쪼갭니다.
아직 모르겠습니다.
다시 레고를 쪼갭니다.
...
...
이제 몇 개인지 눈에 보입니다.
쪼갰던 레고를 합칩니다.
각각의 답도 같이 합칩니다.
쪼갰던 다른 레고를 합칩니다.
각각의 답도 같이 합칩니다.
계속 합칩니다.
...
처음의 레고 작품으로 돌아왔습니다.
이제 이 작품에 레고블럭이 몇 개가 쓰였는지 압니다.

위의 과정을 분할정복(Divide and Conquer)라고 합니다.
재귀호출은 분할정복, 백트레킹 뭐 이런 녀석들이랑 땔래야 땔 수 없는 사이인데요, 이 녀석들의 특징이 주어진 문제를 더 작은 문제로 분할하여 문제를 해결한다는 점에서 동일한 특성을 가지고 있기때문입니다. 실제로 거의 대부분의 경우 D&C나 백트레킹은 재귀함수로 구현하는 경우가 많습니다.


재귀함수(Recursive Function)

재귀적으로 문제를 푸는 함수를 재귀함수라고 하고 직간접적으로 자기자신을 호출합니다.
재귀적으로 문제를 푼다(동일한 형태의 다 작은 부분문제를 풀어나감)는 것을 생각해 봤을 때, 반복이 진행될 때마다 동일한 작업을 해야 한다는 것을 짐작할 수 있습니다.(동일한 형태의 문제를 푸니깐;) 그리고 더 이상 문제를 쪼개지 않아도 되는 상황에 언젠가는 도달해야 합니다. 따라서 재귀함수는 자기자신을 호출하고(동일한 형태) 언젠가는 종료를 해야합니다.


현실적인 예를 들기위해 n!을 재귀적으로 구해보도록 합시다.

여러분은 10!이 얼마인지 아십니까?? 모르겠죠?? 저도 모릅니다. 그래도 10! 은 9!에다가 10을 곱했다는 거는 알 것 같습니다.. 모르시면 중학교 수학책을 찾아보십시오.

10! = 9! * 10

그럼 9!은 얼마죠?? 아직 모르겠네요 하지만 9! = 8! * 9 라는 거는 알겠습니다.

9! = 8! * 9

뭐 이렇게 8!, 7!, ... 점점 내려가다 1!이 되면 답이 1이라는거 바로 알 수 있으니 여기서 재귀를 멈추면 됩니다.

코딩을 하기 위해서는 수식을 일반화할 필요가 있는데요 지금껀 일반화하기 그닥 어렵지 않습니다.

n! = 1 (n == 1 or n == 0)   - 종료조건
    = (n-1) * n (n >= 2)    - 재귀호출

위와 같은 식을 점화식(Recurrence relation)이라고 합니다. 고등학교 수학시간에 수열의 일반항을 구할때 많이 들었던 용어일겁니다. 각설하고 점화식을 알았으면 바로 그래도 코드로 옮겨주면 됩니다.

int fac(int n)   
{   
    if (n <= 1) return 1;   
    return n * fac(n-1);   
}  
​

int fac(int n) { if (n <= 1) return 1; return n * fac(n-1); }

제가 주로 사용하는 언어가 C++인 관계로 C++로 코딩했습니다. 뭐 근데 생각해보니 저 함수는 자바나 C#으로 짜도 저렇게 나오겠네요 쿨럭; 여튼 앞으로도 계속 C++로 작성하겠습니다.

호출이 일어나는 순서를 도식화 하면 더 알기 쉽겠죠?
fac(5)를 호출했을 때 상태의 변화를 도식화하면 아래와 같습니다.

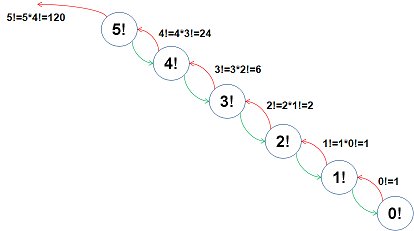
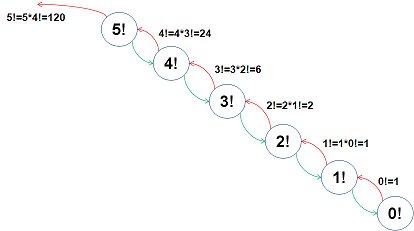
뭐 여기까지 이미 다 알고계신 내용이었을테구요..

재귀함수를 작성하다 보면 의도하지 않은 크리티컬한 문제에 봉착하게 되는 경우가 있습니다. 아래의 예를 봅시다.

공대를 다니면서 절대 피할수 없는 수열이 있습니다. 바로 피보나치수열인데요. 점화식은 아래와 같습니다.

 

점화식대로 재귀함수를 코딩하면 이렇게 나오죠

int fib(int n) { if (n <= 1) return n; return fib(n-1) + fib(n-2); }

int fib(int n)   
{   
    if (n <= 1) return n;   
    return fib(n-1) + fib(n-2);   
}  
​

그런데 여기에 엄청난 문제가 있습니다.. 눈치 채셨습니까??
함수의 콜 상태를 도식화 해보면 이렇습니다.

이 엄청난 문제 눈치채셧습니까??
네 그렇습니다. 그림을 너무 성의없게 그렸군요 죄송합니다 ㅠㅠ

그림을 잘 보면 fib(3)이 두번 계산 되는걸 알 수 있습니다. fib(2)는 3번이구요 fib(1)은 5번이나 호출되네요..
저게 fib(5)를 구하는 그림이라 그렇지 fib(50)을 구한다고 생각해보십시오.. 끔찍합니다..
분석을 해보면 저런식으로 함수를 구현하게 되면 fib(n)을 구하는데 대략 2^n번의 함수 호출이 발생합니다. fib(50)을 구한다면??또 이 표현 안할수가 없네요. 지구가 멸망할때까지 답을 못봅니다

다행이도 이런 문제를 해결하는 Memoization이라는 기법(Memorization이 아닙니다)이 있는데요, 언젠가 포스팅을 하겠습니다.



하노이의 탑

마지막으로 하노이 탑을 옮겨보도록 하겠습니다.

 하노이의 탑 하러가기

하노이의 탑은 세개의 공간 중 한 공간에 쌓여진 탑을 한 번에 하나의 층만 이동하여 다른 공간으로 이동하는 문제인데요 이동하는 도중에 크기가 더 큰 층이 작은 층 위에 올라올 수 없습니다.
최소의 횟수로 하노이의 탑을 옮기는 방법은 단 한가지가 존재하는데 옮기는 횟수가 무려 2^n-1 번이나 됩니다.
인도의 베레니스에 있는 한 사원에  64층의 하노이 탑이 있는데 이 탑을 위의 규칙에따라 옮기면 탑은 무너지고 세상은 종말한다라는 예언이 전해오는데요.. 사실 64층의 탑을 사람의 힘으로 옮기려면 영겁의 세월이 걸립니다. 그 전에 세상이 종말하겠죠;

그럼 본격적으로 하노이 탑을 옮겨보도록 하겠습니다.

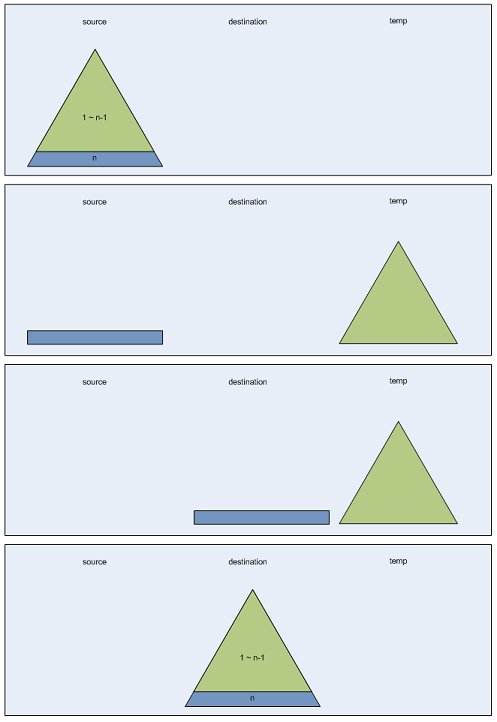
source(S)에 있는 n층의 하노이탑을 destination(D)으로 옮기고자 합니다. 그리고 이를 위해 temp(T)라는 공간이 준비되어 있습니다.
크게 생각해보면 n층의 하노이 탑을 옮기려면 n-1층까지 모든 블록을 S->T로 옮기고 젤 마지막 조각을 S->D로 옮긴 다음에 T에 있는 n-1층의 하노이탑을 D위에 쌓으면 됩니다. 그럼 여기에서 n-1층의 하노이 탑을 옮기는 과정(S->T, T->D)이 필요한데, 이 과정은 n층의 하노이 탑을 옮기는 과정과 방법이 같습니다.
우선 n-1층의 탑을 S->T로 옮기는 것을 생각해봅시다. 이경우 S가 원본이되고 T가 목적지가 됩니다. 각각 S'과 D'이라고 하고 남은 슬롯인 D를 이 경우에서는 임시공간으로 사용하므로 T'이라하면, 우선 n-2층까지 S'->T'으로 옮기고 n-1층을 S'->D'으로 옮깁니다. 그 후 T'에 있는 n-2층까지의 블록을 D'위로 옮겨놓으면 됩니다. 여기에서 또 n-2층을 옮기는 방법을 알아야 하는데요 n-1층을 옮기는 방법과 똑같이 하면 됩니다. 이 과정을 1층이 될때까지 재귀적으로 수행하면 됩니다.

이제 위의 과정을 함수로 작성해봅시다.

함수 TowerOfHanoi(int n, int a, int b, int c) 을 n층의 하노이이 탑을 a에서 b로 c의 임시공간을 이용해서 옮기는 함수라고 정의하면 함수의 몸체는 위에서 설명한 세단계(n-1층까지 a->c로 옮김, n층을 a->b로 옮김, n-1층까지 c->b로 옮김)으로 구성됩니다. 이 세 단계를 모두 재귀호출을 이용하여 구현하면 하노이의 탑은 아래와 같이 간단하게 구현됩니다.

// 하노이의 탑 // n층의 탑을 a에서 b로 옮긴다. c는 여유공간 void TowerOfHanoi(int n, int a, int b, int c) { // 종료조건 if (n == 1) { printf("%d -> %d\n", a, b); return; } // 1~n-1층까지 a->c로 옮긴다 TowerOfHanoi(n-1, a, c, b); // n번째 층을 a->b로 옮긴다 TowerOfHanoi(1, a, b, c); // 1~n-1층까지 c->b로 옮긴다 TowerOfHanoi(n-1, c, b, a); }

// 하노이의 탑   
// n층의 탑을 a에서 b로 옮긴다. c는 여유공간   
void TowerOfHanoi(int n, int a, int b, int c)   
{   
    // 종료조건   
    if (n == 1)    
    {   
        printf("%d -> %d\n", a, b);   
        return;   
    }   
  
    // 1~n-1층까지 a->c로 옮긴다    
    TowerOfHanoi(n-1, a, c, b);   
  
    // n번째 층을 a->b로 옮긴다   
    TowerOfHanoi(1, a, b, c);   
  
    // 1~n-1층까지 c->b로 옮긴다   
    TowerOfHanoi(n-1, c, b, a);   
}