알고리즘 코딩기법 - 7. Bit 연산 Brute Force

안녕하세요 조일룡입니다.

이번에는 2진수를 이용하여 모든 경우의 수를 탐색하는 Brute Force에 대해 알아보겠습니다.


Brute Force

Brute Force는 문제를 해결할 수 있을지도 모를 모든 후보 해를 전부다 탐색하여 정말로 문제를 풀 수 있는 해를 찾는 방법입니다. 쉽게 생각해서 문제가 1 + x = 100 인 경우 이 문제의 해 x가 [0, 100] 사이의 자연수라는 것을 안다고 가정했을 때 단순히 x에 0부터 100까지 모두 대입해 보고 문제가 풀리는 x값을 찾는식의 방법입니다. 물론 저 문제를 저렇게 푸는 바보는 없어야 하겠죠?

여튼 위의 '예' 처럼 Brute Force는 해법이 간단하고 쉬운 반면 모든 후보해를 탐색해야하기 때문에 상당히 느리다라는 단점이 있습니다. 그럼에도 Brute Force를 간간히 사용하는 이유는 쉽기 때문이죠.. 그리고 모든 경우를 따지지 않고서는 도저히 해를 찾지 못하는 문제도 존재합니다.


Basic Algorithm

Brute Force를 구현하는 기본 골격을 살펴보겠습니다.

1. 1. first (P): generate a first candidate solution for P.
   2. next (P, c): generate the next candidate for P after the current one c.
   3. valid (P, c): check whether candidate c is a solution for P.
   4. output (P, c): use the solution c of P as appropriate to the application

   c 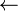first(P)
   while c Λ do
     if valid(P,c) then output(P, c)
     c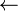 next(P,c)
   
   

Combinatorial explosion

안타깝게도 Brute Force는 입력크기가 커지면 사용하지 못하는 경우가 많습니다. (느리기 때문이지요)

최악의 경우

100 명의 사람들을 최적의 순으로 줄을 세우는 경우를 생각해봅시다. (어떤 경우가 최적인지는 일단 논외로 하겠습니다) 이런 문제에선 모든 경우가 몇 가지나 될까요... 100명의 사람을 순서대로 줄을 세운다.... 고등학교 때 배운 기억이... 나시나요??
기억을 더듬어보니 수학책에서 n 개의 사탕 중 r개를 순서대로 선택하는 경우의 수 nPr = n! / (n-r)! 을 본 적 있는것 같습니다.
100명의 사람중 100명을 순서대로 줄 세우는 경우의 수 = 100 P 100 = 100! / (100-100)! = 100! 이네요!!!!

경우의 수가 이처럼 팩토리얼로 나오면 입력크기가 10이 넘어가면 일반 PC로는 시간이 기하급수적으로 느려집니다. 참고로 10! = 3,628,800 입니다. 정말 참을성이 대단하더라도 입력크기가 15가 되면 15! = 1,307,674,368,000 가 되어 며칠동안 눈뜨고 기다려야 답을 볼 수 있습니다... 흠... 몇년이 될지도 모르겠네요


다른 경우를 생각해봅시다.

당신은 로또를 좋아합니다. 어디선가 잡지를 보니 로또 번호 조합에 따른 당첨 확률 계산공식이 나와 있습니다. 당신은 모든 로또 조합의 경우의 수 중 최고의 당첨 확률을 가지는 번호를 고르고 싶습니다. 한번 Brute Force로 풀어봅시다.
역시 모든 경우의 수를 따져야 하겠습니다. 로또는 45개 숫자 중 6개를 선택하죠.. 맞나요? 다시 고등학교 수학시간으로 돌아가서 n개의 사탕 중 r개를 순서에 상관없이 고르는 경우의 수는.... nCr = n! / ((n-r)! * r!) 이었군요..
45개의 숫자 중 6개를 고르는 경우의 수는 45 C 6 = (45 * 44 * 43 * 42 * 41 * 40) / (6 * 5 * 4 * 3 * 2 * 1) = 8,145,060 이네요..
뭐 이정도는 그나마 PC로 돌릴만 하겠군요....

경우의 수가 조합(Combination)으로 나오면 계산기로 간단히 계산을 해보고 이게 해뜨기전(?!)에 답을 볼 수 있는지 확인한 후 코딩을 시작해야겠습니다.


비트를 사용할 수 있고 가장 빈번히 발생하는 2^n의 경우

당신은 겁나먼 왕국의 대마법사입니다. 어느날 슈렉의 외모에 질려버린 피오나 공주가 당신에게 마법을 부려 슈렉의 외모를 바꾸고 싶어합니다. 당신은 외모를 바꾸는 n가지 마법을 가지고 있고 i번째 마법은 슈렉의 외모를 score(i)만큼 변화 시킬 것입니다. (score(i)는 음수일 수도 있습니다!!) 각 마법은 서로 독립적으로 작용하고 같은 마법을 두 번 이상 쓰더라도 점수는 한 번만 적용됩니다. 슈렉의 현재 외모 점수는 0점이고 피오나 공주는 슈렉의 외모가 정확히 S점이 되기를 원합니다. 당신은 어떤 마법을 쓰겠습니까??

이런경우 n가지의 마법을 놓고 어떤 마법을 쓰고 어떤 마법을 쓰지 않을지를 결정을 해야하겠습니다. 몇 개의 마법을 쓰는지는 자유이기 때문에 모든 경우의 수는 nC0 + nC1 + nC2 + ... + nCn = 2^n 입니다. 더 쉽게 생각하면 각각의 마법마다 쓰는 경우와 안 쓰는 경우 2가지 선택을 할 수 있는데, 마법이 n개 이므로 모두 곱하면 2^n의 경우의 수가 나옵니다.

바로 이런경우 bit연산을 이용하여 쉽게 문제를 해결할 수 있습니다.

2^20 = 약 100만 이고 2^30은 10억 입니다. PC에서 돌린다고 생각해 봤을 때 이 처럼 경우의 수가 2^n이 나오는 경우 n이 30이 넘어가면 밤샐준비를 해야 하겠습니다. (물론 밤은 PC가 새겠군요;)



Brute Force! Bit 조작해서 풀기

다른 예를 생각할 필요없이 아까전에 피오나가 낸 문제를 가지고 해보겠습니다.

당신이 부릴수 있는 마법이 20개라고 합시다. 그리고 각각의 마법에 따른 용모의 변화가 벡터 score로 넘어옵니다. 마법의 점수 합이 S가 되는 모든 경우에 대해 사용하는 마법의 번호(0~19)를 오름차순으로 출력하는 함수를 작성하겠습니다.
////////////////////////////////////////////////////////////////////// // // void Magic(vector<int> socre, int S) // 슈렉의 외모를 S로 만드는 마법의 조합을 찾는다 // // vector<int> score : i번째 마법이 슈렉의 외모점수를 socre[i]만큼 변화시킨다 // int S : 피오나가 원하는 슈렉의 외모 점수 // void Magic(vector<int> score, int S) { int i = 0, j = 0; int n = score.size(); // 마법의 갯수 // 모든 경우(2^n)를 탐색 for (i = 0; i < (1 << n); i++) { // 사용하는 마법의 점수 합 int sum = 0; // 모든 마법 탐색 for (j = 0; j < n; j++) { // i의 경우 j번째 마법을 사용 하는가? if (i & (1 << j)) { // j번째 사용한다면 점수는 score[j]만큼 변한다. sum += score[j]; } } // 사용한 마법의 점수 합이 S이면 마법 출력 if (sum == S) { // 모든 마법 탐색 for (j = 0; j < n; j++) { // j번째 마법을 사용했으면 출력 if (i & (1 << j)) { cout << j << " "; } } cout << endl; } } }


같은 문제를 DFS로 구현하는 백트레킹(backtracking)으로도 풀 수 있습니다.
////////////////////////////////////////////////////////////////////// // // void MagicBacktrack(vector<int>& score, int S, int index, int use) // 슈렉의 외모를 S로 만드는 마법의 조합을 찾는다(백트레킹) // // vector<int>& score : i번째 마법이 슈렉의 외모점수를 socre[i]만큼 변화시킨다 // int S : 피오나가 원하는 슈렉의 외모 점수 // int index : index 번째의 마법을 사용할지 안할지를 검사함 // int use : use의 i번째 bit가 1이면 i번째 마법을 사용하기로 결정함 // int sum : 사용하기로 한 마법의 점수 합 // void MagicBacktrack(vector<int>& score, int S, int index, int use, int sum) { // 마법의 수 int n = score.size(); // 모든 마법에 대해 선택 여부를 결정했음 if (index == n) { // 선택한 마법의 합이 S -> 선택한 마법을 출력 if (sum == S) { // n개의 마법을 탐샙 for (int i = 0; i < n; i++) { // i번째 마법을 사용하기로 했네요 if (use & (1 << i)) { cout << i << " "; } } cout << endl; } return; } /* 마법점수가 양수만 존재한다면 아래 가지치기로 탐색범위를 줄일 수 있다. if (sum > S) { return; } */ // index 번째 마법을 사용하기로 결정함 MagicBacktrack(score, S, index + 1, use | (1 << index), sum + score[index]); // index 번째 마법을 사용 안하기로 결정함 MagicBacktrack(score, S, index + 1, use, sum); } int main() { // 함수가 잘 도나 테스트 해보는 코드입니다. vector<int> score; score.push_back(15); score.push_back(13); score.push_back(-5); score.push_back(7); score.push_back(55); score.push_back(12); score.push_back(3); score.push_back(1); score.push_back(-11); score.push_back(-6); score.push_back(4); MagicBacktrack(score, 47, 0, 0, 0); }


DFS의 기본은 알고리즘 코딩기법 - 3. 재귀호출을 참고하시면 됩니다. 백트레킹에 대해서는 혹시나 마음이 내키면 포스팅 하겠습니다.