http://acm.pku.edu.cn/JudgeOnline/problem?id=2526
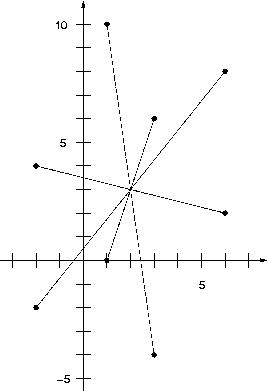 Given is a set of n points with integer coordinates. Your task is to decide whether the set has a center of symmetry.
Given is a set of n points with integer coordinates. Your task is to decide whether the set has a center of symmetry.
A set of points S has the center of symmetry if there exists a point s (not necessarily in S) such that for every point p in S there exists a point q in S such that p-s = s-q.
Description
 Given is a set of n points with integer coordinates. Your task is to decide whether the set has a center of symmetry.
Given is a set of n points with integer coordinates. Your task is to decide whether the set has a center of symmetry. A set of points S has the center of symmetry if there exists a point s (not necessarily in S) such that for every point p in S there exists a point q in S such that p-s = s-q.
Input
The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines contain two integer numbers each which are the x and y coordinates of a point. Every point is unique and we have that -10000000 <= x, y <= 10000000.
Output
For each set of input data print yes if the set of points has a center of symmetry and no otherwise.
Solving
데카르트좌표계에 점들이 있는데 이 점들이 어떤 점을 중심으로 점대칭을 이루고 있는지를 구하는 문제이다.
일단 인풋이 점대칭을 만족한다고 가정한다면 점대칭의 중점의 좌표는 모든 점들의 좌표의 평균좌표를 계산하여 구할 수 있다.
이제 어느 한점을 봤을 때 그 점에 대칭이 되는 점이 있는지 확인해야한다.
가장먼져 드는 생각은 이중루프를 이용하여 확인하는 방법인데 이는 O(n^2)의 시간복잡도로 n이 10000까지 주어지기 때문에 TLE(Time Limit Error)에 걸릴 확률이 높다. 따라서 O(n) 혹은 O(n log n)정도에 문제를 해결해야 한다.
우선 대칭의 중심이 되는 점을 좌표계의 영점에 오도록 모든 점을 평행이동시킨후 각 점들이 x축과 이루는 각도를 계산하여 소팅을 한다. 이 때 arctan 함수를 쓰면 4사분면과 1사분면에 걸쳐 -180~180도의 값을 얻을 수 있고 2사분면과 3사분면에 걸쳐 역시 -180~180도의 값을 얻을 수 있다. 이 각을 이용하여 소팅을 하면(O(n log n)의 시간복잡도) 대칭이 되는 점이 같은 각도를 가지기 때문에 O(n)으로 검색을 하면서 대칭 여부를 확인 할 수 있게 된다. 따라서 최종 시간 복잡도는 O(n log n + n) = O(n log n)으로 n이 10000이라도 충분히 빠른시간내에 계산을 완료 할 수 있다.
Source
Solving
데카르트좌표계에 점들이 있는데 이 점들이 어떤 점을 중심으로 점대칭을 이루고 있는지를 구하는 문제이다.
일단 인풋이 점대칭을 만족한다고 가정한다면 점대칭의 중점의 좌표는 모든 점들의 좌표의 평균좌표를 계산하여 구할 수 있다.
이제 어느 한점을 봤을 때 그 점에 대칭이 되는 점이 있는지 확인해야한다.
가장먼져 드는 생각은 이중루프를 이용하여 확인하는 방법인데 이는 O(n^2)의 시간복잡도로 n이 10000까지 주어지기 때문에 TLE(Time Limit Error)에 걸릴 확률이 높다. 따라서 O(n) 혹은 O(n log n)정도에 문제를 해결해야 한다.
우선 대칭의 중심이 되는 점을 좌표계의 영점에 오도록 모든 점을 평행이동시킨후 각 점들이 x축과 이루는 각도를 계산하여 소팅을 한다. 이 때 arctan 함수를 쓰면 4사분면과 1사분면에 걸쳐 -180~180도의 값을 얻을 수 있고 2사분면과 3사분면에 걸쳐 역시 -180~180도의 값을 얻을 수 있다. 이 각을 이용하여 소팅을 하면(O(n log n)의 시간복잡도) 대칭이 되는 점이 같은 각도를 가지기 때문에 O(n)으로 검색을 하면서 대칭 여부를 확인 할 수 있게 된다. 따라서 최종 시간 복잡도는 O(n log n + n) = O(n log n)으로 n이 10000이라도 충분히 빠른시간내에 계산을 완료 할 수 있다.
'problem solving > Problem Solving' 카테고리의 다른 글
| Ugly Number (0) | 2008.10.06 |
|---|---|
| Subsequence (0) | 2008.10.02 |
| All in All (0) | 2008.10.02 |
| Risk (0) | 2008.10.02 |
| Tug of War (0) | 2008.10.02 |