IPL(Internal Path Length): Binary Tree의 각 노드의 depth의 합
EPL(Extend Path Length): Extended Binary Tree에 새로 추가된 노드들의 depth의 합
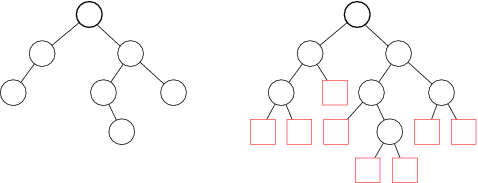
위 그림에서 왼쪽의 트리가 원래의 Binary Tree이고 오른쪽의 트리가 Extended Binary Tree이다.
오른쪽의 트리에서 동그라미로 그려진 노드가 Internal이고 네모로 그려진 노드가 External노드, 즉 원래의 Tree를 Extended Binary Tree로 만들기 위해 추가된 노드들이다.
IPL은 동그라미로 그려진 노드들의 depth의 합으로 위의 그림에서 그 값이 11이 된다.
EPL은 네모로 그려진 노드들의 depth의 합으로 위의 그림에서 그 값은 25이다.
흥미로운 사실은 EPL = IPL + 2n (n: Number of Internal Nodes) 이 성립한다는 것이다.
이를 논리적으로 증명해보자
EPL(Extend Path Length): Extended Binary Tree에 새로 추가된 노드들의 depth의 합

위 그림에서 왼쪽의 트리가 원래의 Binary Tree이고 오른쪽의 트리가 Extended Binary Tree이다.
오른쪽의 트리에서 동그라미로 그려진 노드가 Internal이고 네모로 그려진 노드가 External노드, 즉 원래의 Tree를 Extended Binary Tree로 만들기 위해 추가된 노드들이다.
IPL은 동그라미로 그려진 노드들의 depth의 합으로 위의 그림에서 그 값이 11이 된다.
EPL은 네모로 그려진 노드들의 depth의 합으로 위의 그림에서 그 값은 25이다.
흥미로운 사실은 EPL = IPL + 2n (n: Number of Internal Nodes) 이 성립한다는 것이다.
이를 논리적으로 증명해보자
논리적 추리
하나의 extenal node에 새로운 노드를 추가하여 internal node로 만드는 상황을 생각해보자.
새로 추가되는 노드를 A라고 하고 A의 depth를 d라고 하면 IPL은 d만큼 커진다. 반면 EPL의 경우 지금당장 d의 값을 가진 A가 빠졌기 때문에 d만큼 작아지게 되지만 곧 A가 intenal node가 됨에 따라 A의 양쪽에 위치한 null인 노드들이 external node가 된다. 각각 d+1의 depth를 가지므로 EPL은 다시 2(d+1)이 증가하게 되고 앞에서 없어지 d를 포함하면 EPL은 최종적으로 d+2만큼 증가하게 된다.
즉, 노드가 하나 추가될 때 마다 IPL은 그 노드가 가진 d만큼 증가하고 EPL은 d+2만큼 증가한다. EPL은 IPL보다 항상 2만큼씩 더 증가하는 셈이다.
따라서 n개의 노드가 추가되었을 때 EPL은 IPL보다 2n만큼 클 것이라는 것을 유추할 수 있다.
증명(수학적 귀납법)
EPL = IPL + 2n 을 증명,
1) n = 0 인 경우: IPL + 2n = 0 + 0 = 0 = EPL (성립)
n = 1 인 경우: IPL + 2n = 0 + 2 = 2 = EPL (성립)
2) n = k 인 경우 EPL(k) = IPL(k) + 2k 가 성립한다고 가정하고 k+1일때, EPL(k+1) = IPL(k+1) + 2(k+1)임을 증명,
새로추가되는 노드를 A라고 하고 depth를 d라 하였을 때, 위의 추론에서
따라서,
EPL(k) = IPL(k) + 2k 이 성립하므로 이 식에 대입하면,
따라서, 모든 양수 k에 대해서 EPL = IPL + 2k 가 성립한다.
하나의 extenal node에 새로운 노드를 추가하여 internal node로 만드는 상황을 생각해보자.
새로 추가되는 노드를 A라고 하고 A의 depth를 d라고 하면 IPL은 d만큼 커진다. 반면 EPL의 경우 지금당장 d의 값을 가진 A가 빠졌기 때문에 d만큼 작아지게 되지만 곧 A가 intenal node가 됨에 따라 A의 양쪽에 위치한 null인 노드들이 external node가 된다. 각각 d+1의 depth를 가지므로 EPL은 다시 2(d+1)이 증가하게 되고 앞에서 없어지 d를 포함하면 EPL은 최종적으로 d+2만큼 증가하게 된다.
즉, 노드가 하나 추가될 때 마다 IPL은 그 노드가 가진 d만큼 증가하고 EPL은 d+2만큼 증가한다. EPL은 IPL보다 항상 2만큼씩 더 증가하는 셈이다.
따라서 n개의 노드가 추가되었을 때 EPL은 IPL보다 2n만큼 클 것이라는 것을 유추할 수 있다.
증명(수학적 귀납법)
EPL = IPL + 2n 을 증명,
1) n = 0 인 경우: IPL + 2n = 0 + 0 = 0 = EPL (성립)
n = 1 인 경우: IPL + 2n = 0 + 2 = 2 = EPL (성립)
2) n = k 인 경우 EPL(k) = IPL(k) + 2k 가 성립한다고 가정하고 k+1일때, EPL(k+1) = IPL(k+1) + 2(k+1)임을 증명,
새로추가되는 노드를 A라고 하고 depth를 d라 하였을 때, 위의 추론에서
IPL(k+1) = IPL(k) + d
EPL(k+1) = EPL(k) + d + 2
EPL(k+1) = EPL(k) + d + 2
따라서,
IPL(k) = IPL(k+1) - d
EPL(k) = EPL(k+1) - d - 2
EPL(k) = EPL(k+1) - d - 2
EPL(k) = IPL(k) + 2k 이 성립하므로 이 식에 대입하면,
EPL(k+1) - d - 2 = IPL(k+1) - d + 2k
EPL(k+1) = IPL(k+1) + 2k + 2
EPL(k+1) = IPL(k+1) + 2(k+1)
EPL(k+1) = IPL(k+1) + 2k + 2
EPL(k+1) = IPL(k+1) + 2(k+1)
따라서, 모든 양수 k에 대해서 EPL = IPL + 2k 가 성립한다.
'thoughts > Computer Science' 카테고리의 다른 글
| Paths, Trees, and Flowers presentation (0) | 2010.06.03 |
|---|---|
| Ternary Search (0) | 2008.11.24 |
