Cake Cutting

Description

You are given a rectangular cake of integral dimensions w × h. Your goal is to divide this cake into m rectangular pieces of integral dimensions such that the area of the largest piece is minimal. Each cut must be a straight line parallel to one of the sides of the original cake and must divide a piece of cake into two new pieces of positive area. Note that since a cut divides only a single piece, exactly m − 1 cuts are needed.

If w = 4, h = 4, and m = 4, then the following cuts minimize the area of the largest piece:

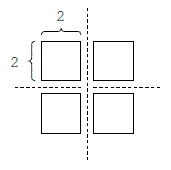
However, if w = 4, h = 4, and m = 3, then the following cuts are optimal:

Input

The input test file will contain multiple test cases, each of which consists of three integers w, h, m separated by a single space, with 1 ≤ w, h, m ≤ 20 and m ≤ wh. The end-of-file is marked by a test case with w = h = m = 0 and should not be processed.

Output

For each test case, write a single line with a positive integer indicating the area of the largest piece.

Source

Stanford Local 2004


Solving

w x h 사이즈의 케익이 있다. 이 케익을 정확히 m-1번 잘라 m개의 조각으로 만들고 싶다. 케익 커팅은 x축과 y축에 평행하게만 자를 수 있고, 한 변의 길이는 반드시 단위길이의 정수배가 되어야 한다. 주어진 케익을 잘라 m개의 조각으로 만들었을 때 가장 큰 케익조각이 최소가 될 때 가장 큰 조각의 크기를 구하시오.

w와 h가 20이하로 주어진다는 점을 생각하면 문제를 접근해보자.

w x h크기의 케익을 자르는 방법은 크게 가로로 자르기와 세로로 자르기, 두 가지 방법이 있다.
가로로 자르는 경우 h-1가지의 방법이 있고 세로로 자르는 경우 w-1가지의 경우가 있다.

m[w][h][m]을 크기가 w x h인 케익을 m-1번 잘라서 만들어 지는 케익 중 가장 큰 케익과 가장 작은 케익의 크기가 가장 작을 때 크기라고 하면 세로로 자를 때 점화식은 다음과 같다.

m[w][h][m] = min(max(m[k][h][c], m[w-k][h][m-c],c=1...m-1), k=1...w-1)

세로로 자르는 경우에도 마찬가지 방법으로 구할 수 있다.

#include <cstdlib> #include <cstdio> #include <vector> #include <algorithm> using namespace std; int main() { int i, j, k; int w, h, m, n; int d[21][21][21] = {0}; for (i = 0; i < 21; i++) for (j = 0; j < 21; j++) for (k = 0; k < 21; k++) d[i][j][k] = 987654321; for (i = 1; i <= 20; i++) { for (j = 1; j <= 20; j++) { d[i][j][1] = i*j; for (k = 2; k <= i*j && k <= 20; k++) { for (m = 1; m < i; m++) { for (n = 1; n < k; n++) { d[i][j][k] = min(d[i][j][k], max(d[m][j][n], d[i-m][j][k-n])); } } for (m = 1; m < j; m++) { for (n = 1; n < k; n++) { d[i][j][k] = min(d[i][j][k], max(d[i][m][n], d[i][j-m][k-n])); } } } } } while (scanf("%d%d%d", &w, &h, &m)) { if (w == 0 && h == 0 && m == 0) break; if (w > h) w ^= h ^= w ^= h; printf("%d\n", d[w][h][m]); } return 0; }