링크
Consider quadratic Diophantine equations of the form:
x2 – Dy2 = 1
For example, when D=13, the minimal solution in x is 6492 – 13![]() 1802 = 1.
1802 = 1.
It can be assumed that there are no solutions in positive integers when D is square.
By finding minimal solutions in x for D = {2, 3, 5, 6, 7}, we obtain the following:
32 – 2![]() 22 = 1
22 = 1
22 – 3![]() 12 = 1
12 = 1
92 – 5![]() 42 = 1
42 = 1
52 – 6![]() 22 = 1
22 = 1
82 – 7![]() 32 = 1
32 = 1
Hence, by considering minimal solutions in x for D ![]() 7, the largest x is obtained when D=5.
7, the largest x is obtained when D=5.
Find the value of D ![]() 1000 in minimal solutions of x for which the largest value of x is obtained.
1000 in minimal solutions of x for which the largest value of x is obtained.
It was hardest problem I had solved from Project Euler ever.
First approach - rather naive one
Algorithm: Check for all integer x >= 2 until the equation hold.
This approach didn't work efficiently because the variable x was only increased by 1.
In case d=61, the minimum possible variable for x is 1766319049. and I couldn't find the number using this algorithm.
Moreover, in case d=661, the smallest x is 16421658242965910275055840472270471049 !! that is the number this problem wants to find and is amazingly enormous number.
This problem cannot be solved by this kind of algorithms(naive algorithms).
To solve this problem, we must find pell's equation.
Second approach - Pell's equation and Continued Fraction
Let 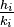 denote the sequence of convergents to the continued fraction for
denote the sequence of convergents to the continued fraction for 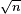 . Then the pair (x1,y1) solving Pell's equation and minimizing x satisfies x1 =hi and y1 = ki for some i. This pair is called the fundamental solution. Thus, the fundamental solution may be found by performing the continued fraction expansion and testing each successive convergent until a solution to Pell's equation is found.
. Then the pair (x1,y1) solving Pell's equation and minimizing x satisfies x1 =hi and y1 = ki for some i. This pair is called the fundamental solution. Thus, the fundamental solution may be found by performing the continued fraction expansion and testing each successive convergent until a solution to Pell's equation is found.
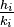 denote the sequence of convergents to the continued fraction for
denote the sequence of convergents to the continued fraction for 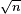 . Then the pair (x1,y1) solving Pell's equation and minimizing x satisfies x1 =hi and y1 = ki for some i. This pair is called the fundamental solution. Thus, the fundamental solution may be found by performing the continued fraction expansion and testing each successive convergent until a solution to Pell's equation is found.
. Then the pair (x1,y1) solving Pell's equation and minimizing x satisfies x1 =hi and y1 = ki for some i. This pair is called the fundamental solution. Thus, the fundamental solution may be found by performing the continued fraction expansion and testing each successive convergent until a solution to Pell's equation is found.-from wikipedia
Once we know the theory, it is easy to implement
python